Skills, Self-Direction, and Applications for Better Math Instruction

There has been much discussion recognizing the critical importance of math instruction and the best ways to engage students. In our research on ways to nurture independent learners, we have developed a pedagogical model that provides some guidance on how to achieve these goals. The Model highlights three core instructional tasks for math teachers to get better performance outcomes in their students.

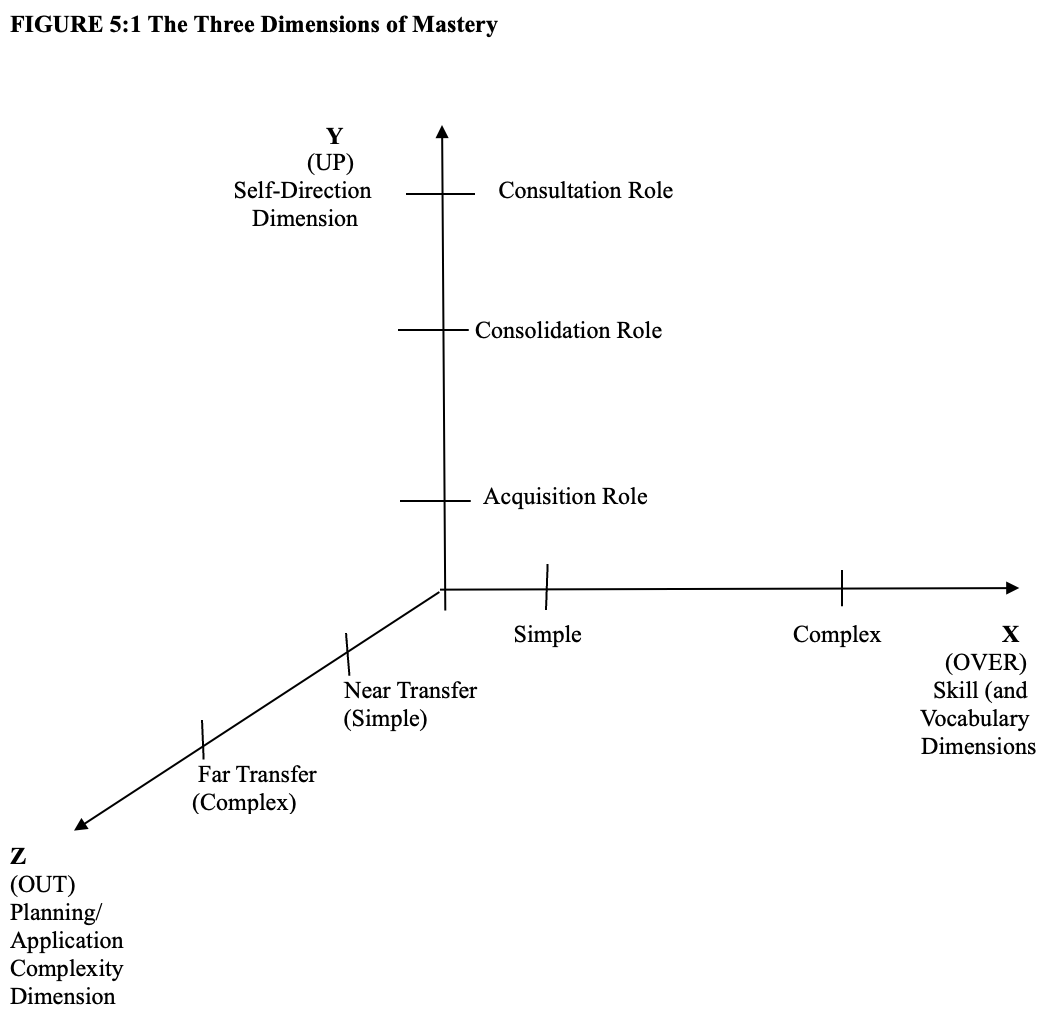
First. Teachers must determine what the simple and later complex Math skills and accompanying understanding that their students need to acquire. At the same time, Math teachers need to make clear to their students "why" they are being asked to learn these skills, and how will they be able to tell if they learned these skills. In order to achieve these pedagogical objectives, teachers need to choose the math tasks carefully along a dimension of varying difficulty skill level. Similar to teaching someone to ski downhill at different levels of difficulty, students in math classes need to be able to choose and work on math tasks that are slightly beyond their current level of competence (a zone of proximal development). Our X axis—Acquiring the Skills and Vocabulary Dimension for Math.

Second. Students must transition between acquiring new math skills, consolidating these new skills through planned practice, and reach the point that they can teach these skills to others and monitor their own performance—i.e. consulting about the newly acquired skills. In order to accomplish these pedagogical objectives, math teachers have to planfully engineer student learning opportunities so their students can move from being novices to developing a level of mastery that frees up the students' mental capacities. The Math teachers will know that their instructional strategies have been effective when their students can not only perform new math tasks, but the students can also teach these skills to others, as well as to themselves. Asking students to incorporate writing. journaling and oral presentation enhance the students’ “expertise”. In short, how can teachers have their students become their own teachers? Our Y axis—Self-Direction Dimension.

Third. Students must become increasingly able to apply new math skills to near transfer (problems similar to instructional examples) and then apply their new skills to more novel problems—far transfer. What do teachers need to do in order to increase that their students will be able and likely to use the math skills on their own over time and settings? How can Math teachers have their students take their voice with them and take ownership of the skills and understanding which were the instruction goals? Our Z axis—Planning/Application Complexity Dimension.

We suggest two strategies to accomplish these objectives:

• One way to do this is for teachers to include "authentic" real life meaningful tasks that require student group collaborative discussion learning math skills need to be a "team sport."
• A second way to increase the likelihood of generalization and maintenance is for math teachers to planfully select transfer tasks that provide students with gradually increasing opportunities to creatively apply what they have learned to new and more distant examples and tasks.

Figure 1 provides a pictorial account of these three tasks. In short, if math teach can move their students across the x axis (the acquiring educational skills dimension), up the y axis (the self-direction dimension), and out and back across the z axis (planning application complexity dimension), their students could have a better chance of becoming more efficient learners.

FIGURE 5:1 The Three Dimensions of Mastery

References:

Biemiller, A., & Meichenbaum, D. (1992/2017). The nature and nurture of student expertise. Educational Leadership 50 (Oct.), 70-75. Reprinted in D. Meichenbaum, The Evolution of Cognitive Behavior Therapy: A Personal and Professional Journey with Don Meichenbaum.

Meichenbaum D. & Biemiller, A. (1998). Nurturing Independent Learners, Helping Students Take Control of Their Education. Cambridge, MA: Brookline Books.

About the authors:

• Andrew Biemiller, Ph.D. is a graduate of Harvard College (B.A.) and Cornell University (M.Sc., Ph.D.). He taught at the Eric Jackman Institute of Child Study, University of Toronto for 36 years. He was responsible for the teacher education program at the Institute for 15 years. His recent research has concerned what word meanings are acquired, the order of meanings acquired, and effective methods of teaching word meanings. His main current research concerns identifying word meanings that are particularly useful for instruction in the early years and primary grades. He published Words Worth Teaching (SRA/McGraw-Hill) in 2010, which summarizes much of this work. In addition, he has published numerous articles and book chapters. He has served as an associate editor of the Journal of Educational Psychology. He has acted as an educational consultant to the U.S. Inst. of Education Science (Dept. of Education), U.S. National Institute of Child and Human Development, publishers (especially SRA/McGraw-Hill), state departments of education, and researchers.
• One of the founders of cognitive behavior therapy, Donald Meichenbaum, Ph.D., was voted among the 10 most influential psychotherapists of the 20th century by North American clinicians. He has presented in all 50 states and internationally. He has published extensively and his most recent book is Roadmap to Resilience has been downloaded by more than 40,000 people in over 130 countries. Other books include Treatment of Individuals with Anger-control Problems and Aggressive Behavior, Treating Adults with Posttraumatic Stress Disorder, Nurturing Independent Learners, and Stress Inoculation Training.

Order a copy of Nurturing Independent Learners by Andrew Biemiller, Ph.D. and Donald Meichenbaum, Ph.D.